행렬(Matrix)은 수학에서 숫자나 변수를 직사각형 배열로 나타낸 것을 의미합니다. 특히 선형대수학에서 중요한 역할을 하며, 경제수학에서도 수요와 공급, 생산 및 소비 등 다양한 경제 모델을 표현하고 분석하는 데 사용됩니다.
1. 행렬의 정의
행렬은 행(row)과 열(column)로 이루어진 2차원 배열입니다. 예를 들어, 다음은 2행 3열의 행렬입니다.
*행(row)은 가로 방향, *열(column)은 세로 방향을 뜻합니다.

행렬의 크기를 나타낼 때는 행의 개수와 열의 개수로 표현합니다. 예를 들어, 위의 행렬은 2×3 크기를 가지며, 첫 번째 숫자(2)는 행의 수, 두 번째 숫자(3)는 열의 수를 의미합니다.
* 서로 같은 행렬의 의미는 두 행렬이 완전히 동일한 형태와 값을 가질 때를 의미합니다.
조건 1) 행과 열의 크기가 같아야 한다
조건 2) 각 대응되는 원소의 값이 같아야 한다
2. 행렬의 연산
1) 행렬의 덧셈과 뺄셈
행렬의 덧셈과 뺄셈은 같은 크기의 행렬들끼리만 가능하며, 대응되는 원소끼리 더하거나 빼는 방식으로 이루어집니다. 이 연산은 행과 열의 크기가 같은 행렬들에서만 수행할 수 있다는 점이 중요합니다.
두 행렬

두 행렬의 덧셈은 아래와 같이 각 원소를 더하는 방식이며, 행렬의 뺄셈은 덧셈과 마찬가지고 각 원소를 빼는 방식입니다.

2) 행렬의 상수배
행렬의 상수배는 행렬의 모든 원소에 동일한 상수를 곱하는 연산입니다.
행렬
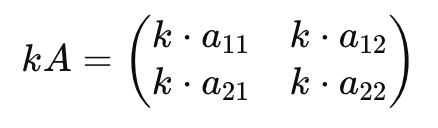
3) 행렬의 곱셈
행렬의 곱셈은 두 행렬을 곱하는 연산으로, 경제수학과 선형대수학에서 매우 중요한 개념입니다.
행렬의 곱셈은 2) 행렬의 상수배와는 규칙이 조금 다릅니다. 두 행렬이 곱해지기 위해서는 반드시 앞 행렬의 열의 수와 뒤 행렬의 행의 수가 같아야 하며, 각 원소를 특정한 규칙에 따라 계산하게 됩니다.
- 행렬
- 만약
계산방법은 행렬

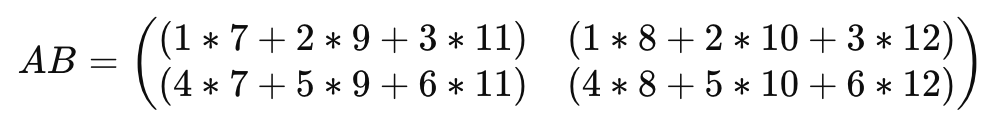
행렬 곱셈은 일반적인 스칼라 곱셈과 다른 몇 가지 특성을 가집니다.
- 교환법칙이 성립하지 않음: A×B≠B×A인 경우가 대부분입니다. 즉, 행렬 곱셈은 순서가 매우 중요합니다.
- 결합법칙: A(B×C)=(A×B)C는 성립합니다.
- 분배법칙: A(B+C)=AB+AC, (A+B)C=AC+BC가 성립합니다.
'경제수학' 카테고리의 다른 글
| 로피탈 정리(L'Hôpital's rule) 정의와 풀이방법 (0) | 2024.11.13 |
|---|
