로피탈 정리(L'Hôpital's rule) 정의와 풀이방법

로피탈 정리(L'Hôpital's Rule)는 미분을 이용해 특정한 형태의 극한을 계산할 때 사용되는 수학적 방법입니다. 주로 함수의 극한이 분수 꼴로 나타나면서 분자와 분모가 각각 0 또는 ∞\∞에 가까워지는 경우, 즉 미정형 0\0​ 또는 ∞\∞​ 형태일 때 유용합니다.

 

1.  로피탈 정리의 정의 

두 함수 f(x)와 g(x)가 특정한 점 a에서 미정형(0\0​ 또는 ∞\∞​)을 만들어 낼 때, 만약 이 두 함수가 a에서 각각 미분 가능하다면, 다음과 같이 계산할 수 있습니다. 

위 식에서 오른쪽 극한이 존재할 경우, 위 식이 성립합니다. 다만 이 법칙을 사용할 때, f(x)와 g(x)의 미분 f′(x)와 g′(x)가 특정 구간 내에서 모두 연속이어야 한다는 조건이 필요합니다.

 

2.  적용 문제 풀어보기

예제문제 1

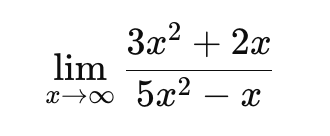
풀이방법

 

1. 미정형 확인: x→∞일 때, 분자와 분모 모두 무한대로 발산하므로 이 극한은 ∞\∞​의 미정형입니다. 따라서 로피탈 정리를 사용할 수 있습니다.

 

2. 분자와 분모를 각각 미분: 로피탈 정리에 따라, 분자와 분모를 각각 미분하여 극한을 다시 구합니다.

• 분자 3x^2 + 2x를 미분하면 6x+2
• 분모 5x^2−x를 미분하면 10x−1

 

 

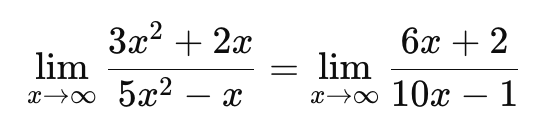
3. 미정형 재확인: 여전히 x→∞에서 분자와 분모 모두 무한대로 발산하므로, ∞\∞​ 형태가 됩니다. 따라서 다시 로피탈 정리를 적용할 수 있습니다.

 

4. 다시 미분 적용: 분자와 분모를 다시 한번 미분합니다.

• 분자 6x+2를 미분하면 6
• 분모 10x−1을 미분하면 10

이렇게 로피탈정리는 반복적으로 사용하여 ∞\∞​꼴의 극한값을 구할 수 있습니다. 

 

예제문제 2

 

로피탈 정리의 주의 사항

• 로피탈 정리는 반드시 분수 꼴의 극한이 미정형 형태 0\0​ 또는 ∞\∞​일 때만 사용할 수 있습니다.
• 필요한 경우, 정리를 반복해서 적용할 수 있습니다. 분자와 분모의 미분이 각각 존재하는지 확인해야 하며, 미분 후에도 미정형이 남으면 다시 적용할 수 있습니다.